Microfluidics and Biofluidics: Precision Engineering for Biomedical Innovation

At PhysAI, we harness the power of microfluidics and biofluidics to revolutionize lab-on-chip technologies for biomedical applications. A cornerstone of this field is the development of mixing devices, which enable precise control over fluid dynamics at the microscale. These systems leverage laminar flow regimes, where the Reynolds number (\( Re \)) is typically low, to achieve efficient mixing through diffusion or chaotic advection. For instance, in a serpentine mixer, the Navier-Stokes equations govern fluid behavior:

\[ \rho \left( \frac{\partial \mathbf{u}}{\partial t} + \mathbf{u} \cdot \nabla \mathbf{u} \right) = -\nabla p + \mu \nabla^2 \mathbf{u} \]

Using COMSOL Multiphysics, we simulate and optimize these devices to ensure uniform reagent distribution—critical for applications like drug formulation and diagnostic assays in the biomedical sector. These tools allow researchers to iterate designs rapidly, reducing development time and costs while enhancing performance in point-of-care testing platforms.

Cell manipulation, sorting, and separation represent another transformative application of biofluidics. Techniques such as dielectrophoresis (DEP), magnetophoresis, and acoustophoresis exploit external fields to control cell trajectories within microfluidic channels. The force exerted by DEP, for example, depends on the Clausius-Mossotti factor and the electric field gradient:

\[ \mathbf{F}_{DEP} = 2\pi r^3 \varepsilon_m Re[K(\omega)] \nabla |\mathbf{E}|^2 \]

Coupled with particle tracking methods, these *phoresis mechanisms enable precise sorting of cells—such as isolating circulating tumor cells (CTCs) from blood samples. COMSOL simulations integrate fluid-structure interactions and field gradients, providing insights into optimizing channel geometries for high-throughput diagnostics, a game-changer for personalized medicine and cancer research.

Pressure and Voltage: Pressure field distribution in an acoustophoresis-based microfluidic channel, simulated using COMSOL Multiphysics. The acoustic field is shown in the flow channel and PDMS containing walls, indicated by the wave color. The electric potential in the piezoelectric base is indicated by the rainbow color. The sinusodial electric potential creates standing waves in the piexo material, which leak into the microfluidics channel resulting in a standing acoustic wave. This acoustic field generates forces on the cells present in the channel, causing them to migrate from regions of high absolute pressure to low. The rate at which this occurs depends on the individual properties of the cells.

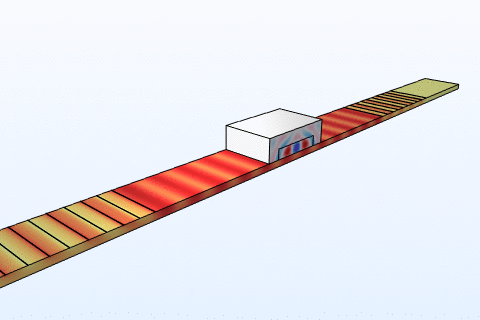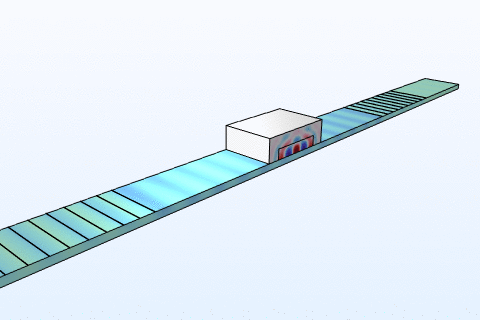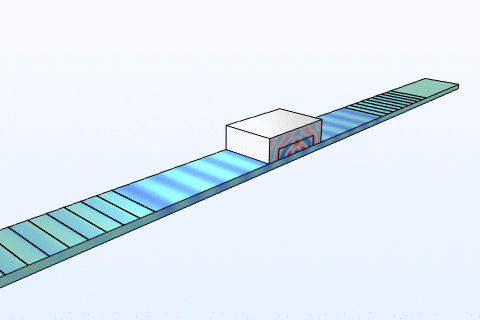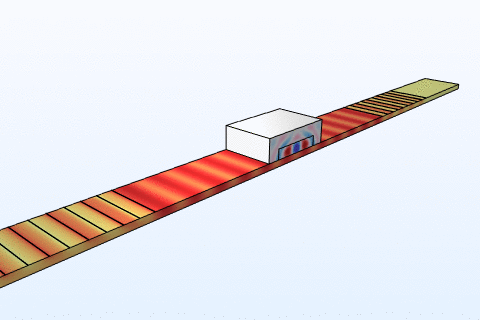
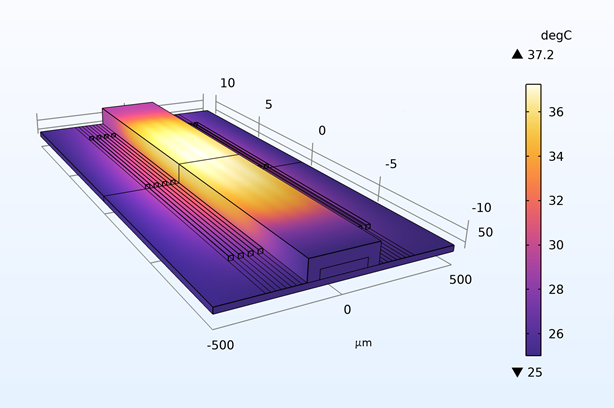
Thermal management is a critical challenge in microfluidic chips, particularly for thermally sensitive bioassays like PCR amplification. Heat transfer in these systems follows the energy equation:

\[ \rho c_p \left( \frac{\partial T}{\partial t} + \mathbf{u} \cdot \nabla T \right) = k \nabla^2 T + Q \]

By modeling convection and conduction with COMSOL, we design chips with integrated microheaters and cooling channels to maintain precise temperature profiles. This ensures reliable performance in enzyme reactions and cell viability studies, addressing needs in clinical diagnostics and bioprocessing industries where temperature control directly impacts yield and accuracy.

Thermal Packaging: The acoustic field needs to be high enough in amplitude to manipulate the cells, which ultimately leads to thermal dissipation. The maximum temperature shown above is 12 degrees above the temperature of the incoming fluid. Thermal gradients can lead to unwanted effects, including influencing the motion of the cells in the channel.

Liquid filling, handling, and dispensing in microfluidics often involve two-phase flows, such as liquid-gas or liquid-liquid systems. Capillary effects dominate at these scales, governed by the Young-Laplace equation:

\[ (\mathbf{T}_1 \cdot \mathbf{n}) - (\mathbf{T}_2 \cdot \mathbf{n}) = \sigma (\nabla_s \cdot \mathbf{n}) \mathbf{n} - \nabla_s \sigma \]

Here, \( \mathbf{T}_1 \) and \( \mathbf{T}_2 \) are the total stress tensors for the two fluids, defined as:

\[ \mathbf{T}_i = -p_i \mathbf{I} + \mu_i \left( \nabla \mathbf{u}_i + (\nabla \mathbf{u}_i)^T \right), \quad i = 1, 2 \]

These dynamics are pivotal for droplet generation and emulsion production, widely used in drug encapsulation and single-cell analysis. COMSOL’s two-phase flow module allows us to fine-tune surface tension and contact angles, optimizing dispensing precision for applications like automated reagent delivery in pharmaceutical R&D. This capability streamlines workflows, enhancing scalability in high-throughput screening.

Aspirate and Dispense: The animation shows the pressure (torr, left), density (middle) and velocity (right) for a generic pipette and well assembly. The pressure and free surface behavior are intimately coupled and oscillations can impact aspiration or dispense precision.

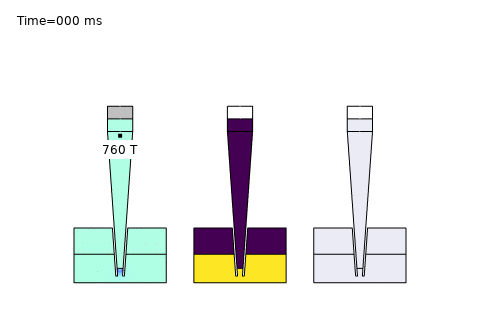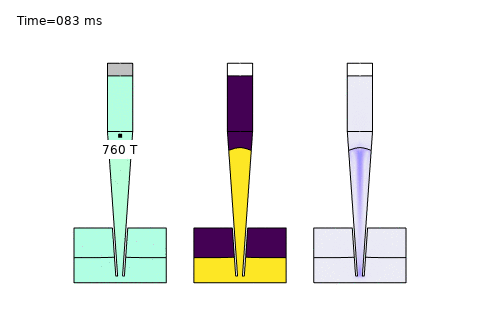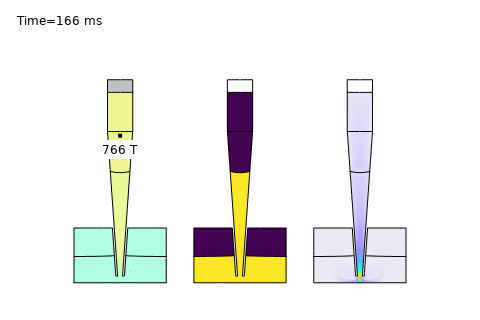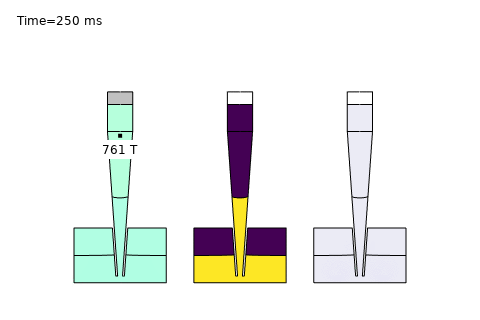
Beyond these core areas, microfluidics is paving the way for cutting-edge applications like single-cell analysis and AI-driven optimization. In single-cell sequencing platforms, precise control of diffusion enables isolation and analysis of individual cells, governed by the Stokes-Einstein relation:

\[ D = \frac{k_B T}{6 \pi \mu r} \]

Here, \( D \) is the diffusion coefficient, \( k_B \) is Boltzmann’s constant, \( T \) is temperature, \( \mu \) is viscosity, and \( r \) is the cell radius. COMSOL simulations optimize channel designs for trapping and analyzing single cells, while AI enhances real-time data interpretation—unlocking breakthroughs in precision medicine and genomics. At PhysAI, we’re pushing these frontiers, delivering innovative solutions that empower biomedical pioneers to transform healthcare.

Cell Separation: The animation shows separation of red blood cells (green) and platelets (blue) along the length of a channel (not to scale). There is a complex balance between the acoustic radiation, drag and Brownian forces. The geometry and applied voltage control the amplitude and spatial distribution of the acoustic field, resulting in a highly complex, coupled system.