Plasma Modeling
Plasma modeling is challenging for even the simplest cases (DC and inductive discharges) due to the complex interaction between the charged particles, neutrals and fields which collectively constitute the plasma. Wave heated discharges add an extra layer of complexity, due to the critical plasma density and capacitively coupled plasmas require a special discretization scheme unique to COMSOL Multiphysics. Equilibrium discharges avoid a lot of the complexity the non-equilibrium cases, but are only valid under certain conditions and present their own unique challenges.
Capacitively Coupled Plasmas (CCPs)
Theoretical Foundations
CCPs rely on an electric field between parallel electrodes, driven by RF power (typically 13.56 MHz). The sheath dynamics are critical, modeled by the Poisson equation:
where \( \phi \) is the electric potential, and \( n_i \) and \( n_e \) are ion and electron densities. The ion flux to the substrate is governed by the Bohm criterion:
where \( u_i \) is the ion velocity, \( k_B \) is Boltzmann’s constant, and \( m_i \) is the ion mass. COMSOL simulates these interactions, optimizing electrode design and gas pressure.
Applications
Semiconductor Industry: CCPs dominate plasma etching (e.g., \( SF_6 \) for silicon) and sputtering for thin-film deposition. Their precise control over ion energy ensures high-aspect-ratio etching, vital for advanced semiconductor nodes. They also neutralize toxic gases like \( NF_3 \).
Other Fields:
- Medical Sterilization: CCPs generate low-temperature plasmas for sterilizing heat-sensitive devices.
- Clean Energy: They support plasma-assisted catalysis for CO₂ reduction.
- Non-Visible Light Sources: CCPs drive neon or argon-based glow discharges for UV and IR applications.

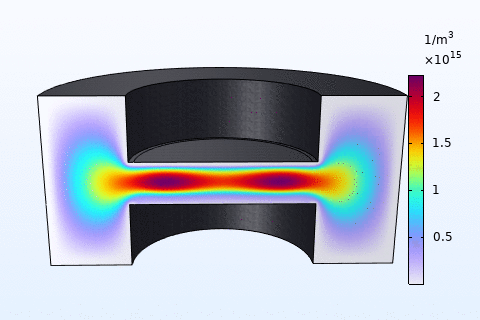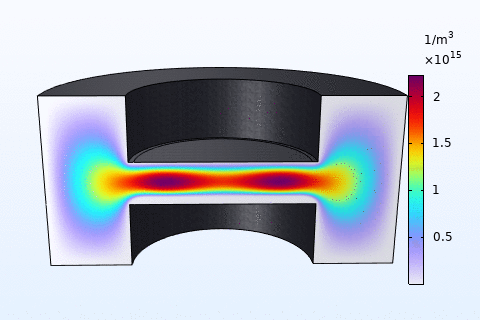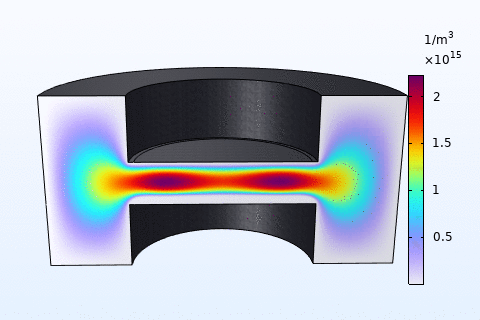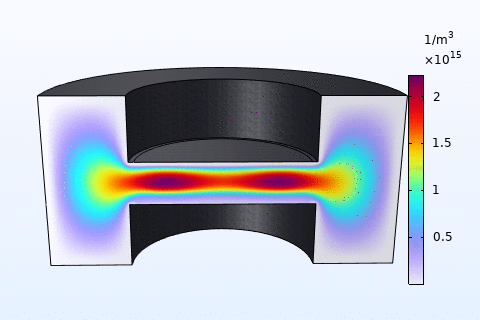
Microwave Plasmas
Theoretical Foundations
Microwave plasmas are sustained by electromagnetic waves, typically at 2.45 GHz, interacting with gas molecules. The wave propagation is described by the vector Helmholtz equation and plasma permittivity \( \epsilon_p \) given by:
Here, \( \omega_p = \sqrt{n_e e^2 / (m_e \epsilon_0)} \) is the plasma frequency, and \( \nu \) is the collision frequency. COMSOL models these dynamics, capturing the transition from microwave absorption to plasma ignition.
Applications
Semiconductor Industry: Microwave plasmas enable high-rate deposition of diamond-like carbon (DLC) films, used as protective coatings in chip manufacturing. Their ability to operate at low pressures enhances control over reactive gas generation (e.g., \( CH_4 \)-based radicals).
Other Fields:
- Medical Sterilization: High-density microwave plasmas sterilize surfaces via UV emission and radical production.
- Clean Energy: They drive hydrogen production via methane reforming, a step toward sustainable fuels.
- Non-Visible Light Sources: Microwave plasmas power excimer lamps, emitting UV for photolithography.
Inductively Coupled Plasmas (ICPs)
Theoretical Foundations
ICPs are generated by an oscillating magnetic field from a coil, inducing electric currents in the plasma. The power transfer is governed by Faraday’s law and Maxwell’s equations, with the induced electric field \( E \) satisfying:
where \( B \) is the magnetic flux density.
Applications
Semiconductor Industry: ICPs excel in plasma etching and deposition for microchip fabrication. Their high electron density (up to \( 10^{18} \, \text{m}^{-3} \)) ensures uniform reactive ion etching (RIE) of silicon wafers, critical for nanoscale features. They also generate reactive gases (e.g., \( CF_4 \)) and destroy toxic byproducts like perfluorocarbons.
Other Fields:
- Medical Sterilization: ICPs produce reactive oxygen and nitrogen species (ROS/RNS) to sterilize equipment without heat damage.
- Clean Energy: They facilitate plasma-enhanced chemical vapor deposition (PECVD) for solar cell production.
- Non-Visible Light Sources: ICPs power UV lamps for water purification.
